Attention Summary

这篇论文主要对 attention 机制做了改进，为此作者总结了 MC 任务上过去常用的三类 attention：

Attention Reader。通过动态 attention 机制从文本中提取相关信息（context vector），再依据该信息给出预测结果。
代表论文：Bahdanau et al. 2015, Hermann et al. 2015, Chen et al. 2016, Wang & Jiang 2016
Attention-Sum Reader。只计算一次 attention weights，然后直接喂给输出层做最后的预测，也就是利用 attention 机制直接获取文本中各位置作为答案的概率，和 pointer network 类似的思想，效果很依赖对 query 的表示
代表论文：Kadlec et al. 2016, Cui et al. 2016
Multi-hop Attention。计算多次 attention
代表论文：Memory Network(Weston et al., 2015)，Sordoni et al., 2016; Dhingra et al., 2016., Shen et al. 2016.

在此基础上，作者对注意力机制做出了改进，具体 BiDAF attention 的特点如下：

并没有把 context 编码进固定大小的 vector，而是让 vector 可以流动，减少早期加权和的信息损失
Memory-less，在每一个时刻，仅仅对 query 和当前时刻的 context paragraph 进行计算，并不直接依赖上一时刻的 attention，这使得后面的 attention 计算不会受到之前错误的 attention 信息的影响
计算了 query-to-context（Q2C）和 context-to-query（C2Q）两个方向的 attention 信息，认为 C2Q 和 Q2C 实际上能够相互补充。实验发现模型在开发集上去掉 C2Q 与去掉 Q2C 相比，分别下降了 12 和 10 个百分点，显然 C2Q 这个方向上的 attention 更为重要

Model Architecture

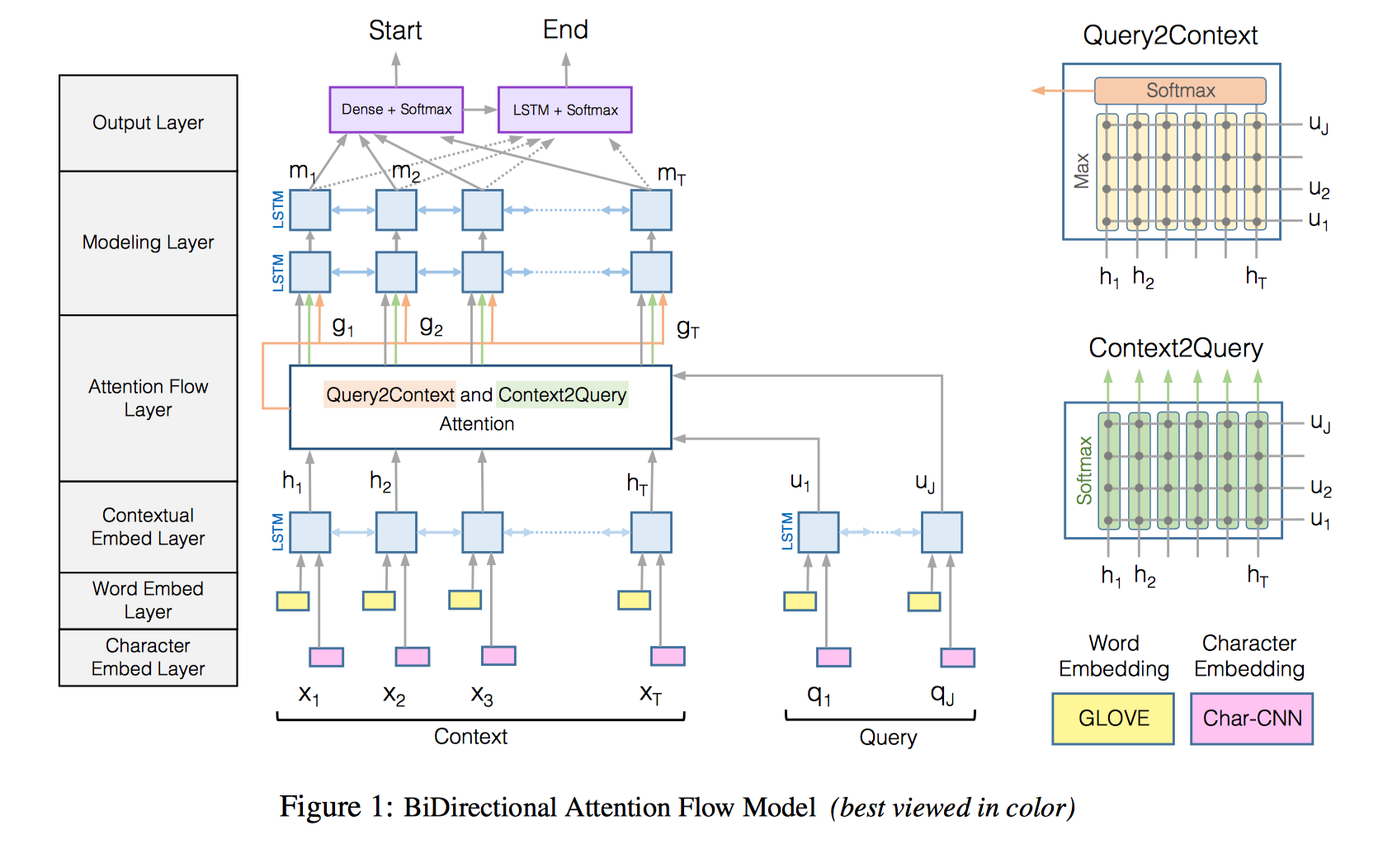
论文提出的是六层结构：
Character Embedding Layer -> Word Embedding Layer -> Contextual Embedding Layer -> Attention Flow Layer -> Modeling Layer -> Output Layer

然而我还是压缩成五层结构来讲吧：

Input embedding layer = Character Embedding Layer + Word Embedding Layer
和其他模型差不多，word embedding + character embedding，预训练词向量，OOV 和字向量可训练，字向量用 CNN 训练
单词 w 的表示由词向量和字向量的拼接然后经过两层 highway network 得到，得到 context vector $X \in R^{d*T}$ 和 query vector $Q \in R^{d*J}$
Embedding encoder layer = Contextual Embedding Layer
对上一步的结果 X 和 Q 分别使用 Bi-LSTM 编码，捕捉 X 和 Q 各自单词间的局部关系，拼接双向 LSTM 的输出，得到 $H \in R^{2d*T}$ 和 $U \in R^{2d*J}$
这前面的两层（or 原文三层）用来捕捉 query 和 context 各自不同粒度（character, word, phrase）上的特征
Context-query attention layer = Attention Flow Layer

The attention flow layer is not used to summarize the query and context into single feature vectors. instead, the attention vector at each time step, along with the embeddings from previous layers, are allowed to flow through to the subsequent modeling layer. This reduces the information loss caused by early summarization.

输入是 H 和 U，输出是 context words 的 query-aware vector G，以及上一层传下来的 contextual embeddings。做 context-to-query 以及 query-to-context 两个方向的 attention。做法还是一样，先计算相关性矩阵，再归一化计算 attention 分数，最后与原始矩阵相乘得到修正的向量矩阵。
c2q 和 q2c 共享相似度矩阵，$S \in R^{T*J}$，相似度计算方式是：
$$S_{tj}=\alpha(H_{:t}, U_{:j}) \in R$$
$$\alpha(h,u)=w^T_{(S)}[h;u;h⊙u]$$
$S_{tj}$ : 第 t 个 context word 和第 j 个 query word 之间的相似度
$\alpha$: scalar function
$H_{:t}$: H 的第 t 个列向量
$U_{:j}$：U 的第 j 个列向量
⊙：element-wise multiplication
[;]：向量在行上的拼接
- context-to-query attention(C2Q): 计算对每一个 context word 而言哪些 query words 和它最相关。前面得到了相关性矩阵，现在 softmax 对列归一化然后计算 query 向量加权和得到 $\hat U$
  $$a_t=softmax(S_{t:}) \in R^J$$
  $$\hat U_{:t}=\sum_ja_{tj}U_{:j}$$
- query-to-context attention(Q2C): 计算对每一个 query word 而言哪些 context words 和它最相关，这些 context words 对回答问题很重要。取相关性矩阵每列最大值，对其进行 softmax 归一化计算 context 向量加权和，然后 tile T 次得到 $\hat H \in R^{2d*T}$。
  $$b=softmax(max_{col}(S)) \in R^T$$
  $$\hat h=\sum_tb_tH_{:t} \in R^{2d}$$
  $\hat U$ 和 $\hat H$ 都是 2dxT 的矩阵
  将三个矩阵拼接起来得到 G
  $$G_{:t}=\beta (H_{:t}, \hat U_{:t}, \hat H_{:t}) \in R^{d_G}$$
  $\beta$ 可以是多层 perceptron，不过如上简单的拼接效果也不错。
  $$\beta(h, \hat u, \hat h)=[h;\hat u; h⊙\hat u; h⊙\hat h] \in R^{8d*T}$$
  于是就得到了 context 中单词的 query-aware representation。
Model encoder layer = Modeling Layer
输入是 G，再经过一次 Bi-LSTM 得到 $M \in r^{2D * T}$，捕捉的是 interaction among the context words conditioned on the query
M 的每一个列向量都包含了对应单词关于整个 context 和 query 的上下文信息
Output layer
预测开始位置 p1 和结束位置 p2
$$p_1=softmax(W^T_{(p^1)}[G; M]), \ \ \ p_2=softmax(W^T_{(p^2)}[G; M^2])$$
M 再经过一个 Bi-LSTM 得到 $M^2 \in R^{2d * T}$，用来得到结束位置的概率分布

最后的目标函数：
$$L(\theta)=-{1 \over N} \sum^N_i[log(p^1_{y_i^1})+log(p^2_{y_i^2})]$$
$y^1_i$ 和 $y^2_i$ 分别是第 i 个样本的 groundtruth 的开始和结束位置